Nota: il simbolo * indica moltiplicazione; x^n indica la potenza n-esima di x, p.es. x^2 significa "x al quadrato"

Esercizio 1

Un blocco di ghiaccio di massa mg = 0,475 Kg è posto all’interno di una pentola senza coperchio di capacità termica Cp = 310 J/K. Inizialmente il sistema si trova ad una temperatura T0 = –10,3 °C e viene poi riscaldato da un fornello che fornisce una quantità di calore Q = 21,7 Kcal.

Calore specifico del ghiaccio: 

cg = 2100 J/(Kg·°C )
Calore latente di fusione del ghiaccio: Lf = 333 KJ/Kg

1 cal = 4,186 J

  • a)  Determinare la capacità termica del solo blocco di ghiaccio.

La capacità termica è data dal prodotto del calore specifico per la massa: 

Cg = mg * cg = 997 J/Kg

  • b)  Determinare la capacità termica totale del sistema.

Il sistema che scaldiamo è composto dalla pentola e dal ghiaccio:

Cs = Cp + Cg = 1307 J/Kg

  • c)  Calcolare la quantità di calore necessaria per portare tutto il sistema alla temperatura di 0 °C prima che il ghiaccio inizi a fondersi.

Siccome il riscaldamento da T0 a T1 = 0 °C non coinvolge nessuna trasformazione di fase, il calore necessario Q0 è dato dal prodotto della capacità termica Cp del sistema per la differenza di temperatura ∆T = T1 - T0 = (0 °C - (–10,3 °C) ) = 10,3 °C, quindi Q0 = Cs * ∆T = 13500 J

  • d)  Quanto ghiaccio si sarà fuso alla fine del processo di riscaldamento?

La quantità di calore trasferita nel riscaldamento è Q = 21,7 Kcal = 90800 J. Di questi, Q0 sono stati usati per riscaldare il sistema a T1 = 0 °C. I rimanenti Q1 = Q - Q0 = 77300 J causano lo scioglimento di una certa parte di ghiaccio mf = Q1 / Lf = 0,232 Kg.

  • e)  Nell’ipotesi in cui il calore venga fornito in un arco di tempo di 10,0 minuti a potenza costante, dopo quanto tempo dall’inizio del riscaldamento il ghiaccio inizia a fondere?
L'energia termica totale Q è fornita in un tempo t = 600 s, quindi ad una potenza P = Q/t = 151 W. Siccome il ghiaccio inizia a fondere dopo che sono stati somministrati Q0 = 13500 J, il tempo richiesto vale t0 = Q0 / P = 89,0 s.

Esercizio 2

Un contenitore per alimenti è mantenuto ad una temperatura interna di -18 °C da una macchina termica che funziona da frigorifero. In t = 6,00 minuti il consumo di energia elettrica per far funzionare il frigorifero è W = 2940 J. Supponendo che la temperatura esterna sia di 27 °C e che il frigorifero compia trasformazioni reversibili ed abbia quindi efficienza massima,

  • a)  Determinare l’efficienza del frigorifero.
L'efficienza η di un frigorifero è il rapporto tra calore Q1 sottratto dal reparto interno del frigo ed il lavoro W fornito per farlo funzionare: η = Q1/W. L'efficienza teorica massima è data dal rapporto η_max = T1 / (T2-T1), in cui le temperature sono  temperature assolute, cioè espresse in Kelvin: T1 = (273-18)K = 255 K, T2 = (273+27)K = 300 K, T2 - T1 = 45 K, quindi η_max = 5,67. Siccome in questo problema si suppone efficienza massima, η = 5,67. 

  • b)  Calcolare il calore sottratto all’interno del contenitore.
Q1 = W * η = 16700 J. 

  • c)  Calcolare il calore ceduto all’ambiente.

Il calore ceduto all'ambiente è Q2 = Q1 + W = 19600 J (riportando 3 cifre significative).

  • d)  Se il frigorifero ha un rendimento pari al 50% rispetto a quello ideale, quanto lavoro meccanico è necessario per estrarre dal contenitore la stessa quantità di calore?

Se η' = 50% η_max = 0,5 * η_max = 2,83. Allora W' = Q1 / η' = 5880 J, cioè il doppio di W.

  • e)  La superficie esterna del contenitore ha un’area di A = 1,10 m^2 ed è costituita da un materiale isolante di spessore d = 28 mm. Determinare il coefficiente di conducibilità termica di tale materiale.
Per mantenere il contenitore alla temperatura richiesta, bisogna sottrarre il calore Q1 ogni t = 360 s, quindi nello stesso tempo entra la stessa quantità di calore Qe = Q1 dalle pareti esterne. Dalla formula della conducibilità termica

Qe/t = k * A * ∆T / d ricaviamo che il coefficiente di conducibilità termica vale

k = Qe * d / ( t * A * ∆T ) = 0.0262 J / ( m * s * K)

essendo ∆T = (27 °C- (-18°C) ) = 45 K la differenza di temperatura tra esterno ed interno.


Esercizio 3


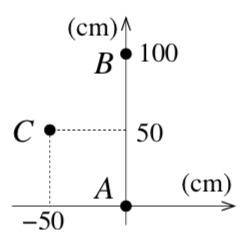
Tre cariche elettriche A,B,C sono poste come in figura. I valori delle cariche sono qA = 6,00 μC, qB = -2,00 μC, qC = -15,0 μC.

k = 8,99 * 10^9 N * m^2 / C^2

  • a) Calcolare la forza elettrostatica che agisce sulla carica C.

Sfruttiamo il principio di sovrapposizione, secondo il quale la forza totale sulla carica C è uguale alla somma delle forze esercitate dalle altre cariche. La distanza tra le cariche A e C vale dAC = 0,707 m, ed è uguale alla distanza dBC tra le cariche B e C. La forza che A esercita su C ha modulo FA = k * |qA * qC| / dAC^2 = 1,62 N, è attrattiva, quindi diretta da C verso A. Le sue componenti sono: FAx = 1,14 N, FAy = -1,14 N. La forza che B esercita su C ha modulo FB = k * |qB * qC| / dBC^2 = 0,54 N, è repulsiva, quindi diretta da B verso C. Le sue componenti sono FBx = -0,38 N, FBy = -0,38 N. La forza totale si ottiene sommando le forze come vettori:

Fx = FAx + FBx = 0,76 N,  Fy = FAy + FBy = -1,53 N.

La carica C viene quindi allontanata ad una distanza grandissima dalle cariche A e B.

  • b) Calcolare il campo elettrico nel punto in cui c’era la carica C.

Per calcolare il campo elettrico nel punto C bisogna sommare i campi elettrici prodotti dalle cariche A e B in quel punto (la carica C essendo molto lontana), procedendo analogamente a quanto fatto nella precedente domanda a). Si può però ottenere il risultato molto più rapidamente ricordando che il campo elettrico in C provoca una forza F = q * E su una carica q posta in C, ossia E = F / q. Usando la F calcolata in a) per q = qC, otteniamo per le componenti di E: Ex = Fx / qC = -5,09 * 10^4 V/m, Ey = Fy / qC = 1,02 * 10^5 V/m.

Alternativamente, e più facilmente, si poteva calcolare il campo elettrico nel punto C generato dalle cariche A e B, e poi, moltiplicando per qC, si otteneva la forza agente sulla carica C.

  • c) Calcolare il potenziale elettrostatico nello stesso punto (considerando nullo il potenziale all’infinito).

Anche per il potenziale ettrostatico vale il principio di sovrapposizione: il potenziale V(C) in C è dato dalla somma dei potenziali prodotti dalle cariche A e B:    VA(C) = k * qA / dAC = 76300 V;   VB(C) = k * qB / dBC = -25400 V;  Il potenziale è una quantità scalare, quindi la somma è semplicemente una somma algebrica (con il segno): V(C) = VA(C) + VB(C) = 50900 V.

  •  d) Determinare il lavoro che è stato necessario fare per allontanare C dalla sua posizione originale.
Il lavoro necessario per spostare un corpo soggetto a sole forze conservative da una posizione r1 ad una posizione r2 è dato da W = U(r2) - U(r1), dove U(r) indica l'energia potenziale nella posizione r. Nel caso della forza elettrostatica sulla carica qC vale
U(r) = qC * V(r), quindi U(r1) = U(C) = qC * V(C) = -0,763 J, U(r2) = qC * (0 V) = 0 J (il potenziale all'infinito vale zero), W = 0 J - (-0,763 J) = 0,763 J.
Che il lavoro sia positivo è naturale: qC < 0 è attratta dal sistema (qA + qB) > 0, quindi bisogna compiere lavoro per allontanare qC.

Esercizio 4

Un generatore di corrente alternata è costituito da un avvolgimento con N = 600 spire di forma circolare e di area A = 0,0120 m^2. L’avvolgimento ruota a velocità angolare ω in un campo magnetico uniforme di intensità B = 0, 333 T. Si vuole ottenere una tensione efficace Veff = 180 V.

  • b) Tra quali valori massimo e minimo varia la tensione?
Nella corrente alternata la tensione varia nel tempo con andamento sinusoidale V(t) = Vmax * sin(ω*t), quindi varia tra +Vmax e -Vmax, e la tensione efficace vale Veff = Vmax/√2. Quindi Vmax = Veff * √2 = 255 V. 

  • a) Quanto deve valere la velocità angolare ω dell’avvolgimento?
La tensione massima fornita da un generatore di tensione alternata vale Vmax = N*A*B*ω. Quindi ω = Vmax / (N*A*B) = 106 rad/s.

Il generatore viene quindi collegato ad un circuito composto da due resistenze in parallelo del valore di R1 =500 Ω ed R2 =700 Ω.

  • c) Quanto vale la corrente di picco prodotta dal generatore?
Due resistenze in parallelo sono equivalenti ad un'unica resistenza R = 1 / ( 1/R1 + 1/R2 ) = 292 Ω. La corrente di picco, cioè la corrente massima, vale Imax = Vmax / R = 0,872 A.
  • d) Qual è la potenza media erogata dal generatore? Si trascuri la resistenza interna del generatore.

La potenza media, o efficace, è Peff = Veff^2 / R = 111 W.

  • e) Quanto vale il momento torcente (medio) necessario per far girare il generatore?

In un moto rotatorio, la potenza è data dal prodotto del momento torcente τ e della velocità angolare ω: P = τ*ω. Siccome viene richiesto il momento torcente medio, usiamo la potenza media: <τ> = Peff / ω = 1,05 N*m.


Esercizio 5

Un proiettore di diapositive ha una lente convergente di distanza focale f = 50,00 mm. Una diapositiva viene posta davanti alla lente ad una distanza p = 51,00 mm. Dalla parte opposta della lente viene posto uno schermo.

  • a)  A quale distanza dalla lente deve essere posto lo schermo affinché si veda nitidamente l’immagine prodotta dal proiettore?
La distanza q dell'immagine reale prodotta dalla lente si ricava dalla formula delle lenti
1/p + 1/q = 1/f , quindi q = 1 / ( 1/f - 1/p ) = 2,55 m.
Nota: l'errore relativo sulle misure di f e p vale circa 0,0002, ed è uguale all'errore relativo di 1/f e 1/p. Quindi l'errore assoluto di 1/f ~ 1/p ~ 20 (m^-1) vale 0,004. Siccome 1/f - 1/p = 0,392, l'errore relativo di 1/q (e quindi anche quello di q) vale circa 0,01 (ossia 1%). Quindi q va riportato con al più 3 cifre significative.

  • b)  Quanto vale l’ingrandimento dell’immagine?
L'ingrandimento dell'immagine vale m = q / p = 50,0.
Nota: anche m ha una precisione dell'1% e va riportato con al più 3 cifre significative.
 
  • c)  Per vedere le persone a testa in su, la diapositiva va messa con le persone a testa in su o in giù?
L'immagine reale prodotta da una lente convergente con l'oggetto ad una distanza p > f è rovesciata. Quindi la diapositiva va messa a testa in giù.
 

Per aumentare l’ingrandimento, lo schermo viene allontanato dal proiettore di una distanza d = 1,80 m.

  • d) Di quanto bisogna modificare la posizione della lente per rimettere a fuoco l’immagine?
Spostando lo schermo, non si vede più un'immagine "a fuoco", nitida. Per rendere nitida la visione viene chiesto di spostare la lente. Rispetto a prima variano sia p che q, che ora chiamiamo p' e q', mentre non varia la distanza focale f della lente, che è una sua caratteristica costruttiva. Per avere "a fuoco" la nuova immagine, deve valere 1/p' + 1/q' = 1/f. Sappiamo anche che la distanza tra l'oggetto e l'immagine (p'+q') è aumentata di d = 1,80 m rispetto a prima (p+q = 2,60 m), quindi p'+q' = 4,40 m (indichiamo con d' =4,40 m questa distanza). Il sistema si può risolvere in questo modo: moltiplicando per p' * q' * f l'equazione delle lenti otteniamo l'equazione equivalente  f * ( q' + p' ) = p' * q'. Sostituiamo poi q' = d' - p' e ricaviamo un'equazione di secondo grado per p':  x^2 - d' * x + d' * f = 0  ove x = p' è l'incognita. Si ottengono due soluzioni: la prima soluzione p' = 4,35 m va scartata (perché corrisponde a spostare la lente di 4,30 m per metterla a circa 5 cm dallo schermo); la seconda soluzione p' = 50,58 mm è quella corretta, che corrisponde ad avvicinare di 0,42 mm la lente alla diapositiva: p' - p = -0,42 mm.

Si poteva rispondere a questa domanda anche nel seguente modo, approssimato ma molto più semplice: poiché lo spostamento della lente sarà molto piccolo rispetto alla distanza q' tra la lente e lo schermo, possiamo approssimare q' = q + d = 4,35 m. Allora, sempre dall'equazione delle lenti, dovrà essere p' = ( 1/f - 1/q' ) = 50,58 m, come trovato precedentemente con il metodo esatto (le cifre successive dello sviluppo decimale di p' sono ovviamente diverse).

Modifié le: mercredi 15 juillet 2020, 09:55