Aperçu des sections

  • Généralités

    Tout replier Tout déplier


    Libro di testo: Mazzoldi-Nigro-Voci Elementi di Fisica (EdiSES)

    Raccomando anche il libro Focardi, Massa, Uguzzoni, Villa, Fisica1 (Ambrosiana)

    In allegato degli appunti miei (verranno aggiornati via via)

    Se volete proporre domande per il compito, ecco qui il link https://goo.gl/forms/kmfl4EUxHttxWwgk2

    Esercizi: https://it.wikibooks.org/wiki/Esercizi_di_fisica_con_soluzioni

    Modalità esami simile a quella di Seminara https://www.domenicoseminara.com/ ma non si possono portare appunti e libri (che sono a disposizione sulla cattedra). 

    L' esame scritto si supera con un voto maggiore od uguale a 17.  Gli studenti con una votazione fra  17 e 20 sono obbligati a fare l' orale.   Gli studenti con una votazione maggiore od uguale a 21  sono esonerati dall'orale a meno che non desiderino fare l' orale per migliorare la loro votazione. 

    Il compito è composto da 6 domande (cinematica, dinamica del punto, statica e dinamica dei rigidi, fluidi, termodinamica -- più domande possono far parte dello stesso esercizio) con un punteggio complessivo pari a 36 (6 punti a domanda, ci possono essere domande più semplici fino a 4 punti e domande più difficili fino a 8 punti). 


  • 20/9/2018 Test di fisica intuitiva

    per fare il test andare su https://goo.gl/forms/EyAX641hv4yNxSQE3 o da qui


  • 25/9/2018 Test psicologico e magia della fisica

    Test su pensieri veloci e lenti (Giorgio Gronchi)

    Magia e Fisica (Franco Bagnoli)

    Vedere anche materiale su fisicax.complexworld.net


  • 27/9/2018 Introduzione al corso. Cinematica 1D

    • Introduzione al corso
    • Sistemi di riferimento 3D: cartesiano, polare-cilindrico, polare. trasformazione tra le coordinate
    • Richiami di trigonometria
    • Modello di base: traiettorie continue e "lisce" nello spazio e nel tempo
    • Vettore posizione: expression in coordinate e tramite la lunghezza del percorso (legge oraria)
    • Studio della legge orario: caso lineare. Velocità
    • Legge oraria quadratica: velocità istantanea come derivata rispetto al tempo (esempio). 



  • 2/10/2018 Derivate

    1. Definizione di velocità per moti a velocità costante: S(t) è una equazione lineare in t: 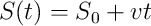S(t)=S_0+vt , rette nel grafico (S,t)
    2. Velocità come coefficiente angolare della tangente al grafico di S(t)
    3. Notazione di funzione: cosa vuol dire il "t" in S(t)
    4. derivata =come limite del rapporto incrementale per \Delta t\rightarrow 0
    5. alcune proprietà dei limiti: limite di una somma, di un prodotto, di funzione di funzione
    6. Notazioni delle derivate: df/dt, f', \dot{f}
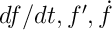
    7. Alcune derivate (potenze, seno, coseno, esponenziale, logaritmo)
    8. Proprietà delle derivate (prodotto, funzione composta, funzione inversa)
    9. Derivata del quoziente
    10. Derivate di funzioni inverse (exponenziale-logaritmo, arcoseno, arcotangente
    11. Numeri complessi in formato cartesiano e polare
    12. Esponenziali complesse, seno e coseno iperbolico, di variabili reali e complesse (cenni). 

  • 4/10/2018 Serie e moto unif. accelerato

    • Moto uniforme in 1D: tempo di collisione 
    • Distanza percorsa
    • Serie di potenze: 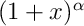(1+x)^\alpha, sen(x), cos(x), tan(x), exp(x), ln(x) e uso con i limiti
    • Serie di potenze: i coefficienti sono le derivate in 0
    • Unità di misura: controllo dimensionale
    • Moto uniformemente accelerato. caduta dei gravi. tempo di collisione
    • Esercizio sul calcolo del tempo di ritorno del suono e limite per velocità del suono infinita.


    SE NON PRENDETE A CAZZOTTI LA TELECAMERA LE RIPRESE VENGONO PIÙ DIRITTE!!!!

  • 9/10/2018 Vettori



    • Vettori come oggetti intrinseci (frecce): somma e sottrazione tra vettori, prodotto scalare
    • Punti del piano come vettori
    • Versori (vettori di norma 1)
    • Prodotto scalare con un versore: proiezione nella direzione
    • I versori degli assi cartesiani.
    • La proiezione lungo gli assi come prodotto scalare con i versori
    • Vettore come somma delle componenti moltiplicate per i versori
    • Prodotto scalare: formula a partire dalle componenti
    • Applicazione: derivare il coseno dell'angolo tra due vettori attraverso il confronto tra formula originale e quella con le componenti
    • La retta come luogo dei punti che hanno la stessa proiezione lungo un versore: confronto con la formula
    • Distanza di una retta dall'origine
    • Distanza di un punti da una retta
    • Prodotto vettoriale tra vettori e tra i versori degli assi
    • Prodotto vettoriale come area del parallelogrammo
    • Prodotto misto e volume di un parallelepipedo


  • 11/10/2018 moto in 2-3D

    • Moto in 2 o 3 D: raggio vettore, velocità, accelerazione
    • Moto parabolico (caduta dei gravi) come composizione di un moto rettilineo uniforme e un moto uniformemente accelerato
    • La velocità è sempre tangente alla traiettoria
    • Tangente ad una curva tramite la definizione di velocità
    • Moto circolare uniforme e non uniforme
    • Velocità ed accelerazione nel moto circolare uniforme
    • Moto circolare uniforme come composizione di due moti armonici in quadratura
    • Moto oscillatorio (sinusoidale): pulsazione, periodo, frequenza, ampiezza
    • Accelerazione centripeta

  • 16/10/2018 Moto circolare e forze

    • Moto circolare uniforme: velocità e accelerazione in coordinate e in notazione intrinseca (derivata del raggio vettore e del vettore velocità)
    • Moto circolare vario: velocità e accelerazione in coordinate e in notazione intrinseca (derivata del raggio vettore e del vettore velocità) Accelerazione centripeta e tangenziale
    • Moto qualsiasi: cerchio osculatoree
    • Esercizio: luogo dei centri dei cerchi osculatori di una parabola (evoluta della parabola)
    • Introduzione alla dinamica: forze, forza peso, forza elastica, funi inestensibili, carrucole


  • 18/10/2018 Leggi di Newton

    • Esercizio di cinematica
    • Dinamica: primo principio. Sistemi di riferimento inerziali
    • Trasformazioni di Galileo
    • Secondo principio di Newton: forze ed accelerazioni
    • Massa inerziale e massa gravitazionale
    • Esperimento di Galileo: equivalenza delle masse. Accelerazione di gravità
    • Terza legge di Newton (azione e reazione)
    • Forze costanti: risoluzione di equazioni differenziali. Moto uniformemente accelerato
    • Moto viscoso (lineare). Equazione differenziale per la velocità. Velocità limite

  • 23/10/2018 Pendolo e oscillatore armonico

    • Esercizio di cinematica
    • Il pendolo matematico come esempio di equazione differenziale non lineare
    • Linearizzazione per piccole oscillazioni: equazione dell'oscillatore armonico
    • Varie rappresentazioni: combinazione di seno e coseno o esponenziali complessi
    • Il ruolo delle condizioni iniziali
    • Accelerazione tangenziale e centripeta nel pendolo matematico (piccole oscillazioni)
    • Tensione della fune


  • 30/10/210 Oscillazioni smorzate e forzate

    • Oscillatore armonico: formulazione generale
    • Soluzione dell'equazione omogenea: moto oscillatorio smorzato, moto sovrasmorzato, moto critico
    • Forzante sinusoidale: soluzione particolare
    • Condizioni di risonanza
    • Attrito radente: modello microscopico, indipendenza dalla superficie di contatto, attrito statico e dinamico. 

  • 6/11/2018 Integrali. Quantità di moto. Momenti

    1. Integrali. Definizione. Esempi
    2. Integrali come funzioni degli estremi.
    3. Integrali per parti e per sostituzione.
    4. Impulso di una forza e quantità di moto.
    5. Sistemi a massa variabile. Forze come derivata della quantità di moto.
    6. Momento di un vettore. Momento di una forza.
    7. Momento della quantità di moto (momento angolare). 
    8. Momento di una forza come derivata del momento angolare. 
    9. Pendolo balistico. 


  • 8/11/2018 Lavoro ed energia

    • Quantità di moto, momento della forza, momento angolare.
    • Energia cinetica
    • Lavoro
    • Teorema delle forze vive. Esempio: moto lungo un piano inclinato. 
    • Campi vettoriali. Gradiente. Linee di livello. 
    • Forze conservative.
    • Lavoro e integrali di linea. 
    • Conservazione dell'energia. Esempi. 
    • Energia potenziale gravitazionale. 
    • Energia potenziale elastica.


  • 13/11/2018 Sistemi di riferimento accelerati

    • Sistemi di riferimento accelerati. Sistema fisso e mobile. Posizione di un punto
    • Derivazione dei versori del sistema di riferimento mobile, vettore velocità angolare.
    • Accelerazione nei sistemi di riferimento mobili. Trascinamento.
    • Forze nei sistemi di riferimento accelerati: forze di inerzia (apparenti). Forze di trascinamento, centrifuga e di Coriolis. 
    • Esempi (video). 

  • 15/11/2018 Dinamica dei sistemi. Centro di massa

    • Dinamica dei sistemi: forze interne ed esterne
    • Centro di massa
    • L'accelerazione del centro di massa dipende solo dalle forze esterne
    • Caso forza-peso: la massa può essere concentrata nel centro di massa
    • Sistemi continui: Densità lineare, di superficie e volumetrica
    • Determinazione del volume/superficie tramite integrale
    • Calcolo del centro di massa di un triangolo, piramide, sfera. 

  • 20/11/2018 Dinamica dei sistemi. Equazioni cardinali, urti

    • Calcolo volume e centro di massa. Densità. Integrali in coordinate cartesiane, polari, cilindriche. 
    • Sistema del centro di massa.
    • Quantità di moto e centro di massa. 
    • Momento della quantità di moto e centro di massa
    • Eneergia cinetica e centro di massa. 


  • 22/11/2018 Dinamica dei rigidi

    • Momento angolare di una coppia di punti materiali legati rigidamente.
    • Momento angolare di una lamina rigida
    • Momento angolare di un corpo 3d: non è in genere diretto come omega.
    • Momento d'inerzia
    • Assi principali d'inerzia
    • Derivata del momento angolare e momento delle forze esterne
    • Equazioni cardinali
    • Pendolo fisico
    • Energia cinetica


  • 27/11/2018 Momento di inerzia

    • Richiamo cinematica dei rigidi
    • Centro di istantanea rotazione
    • Rotolamento senza strisciamento
    • Equazioni cardinali
    • Momento di inerzia di una sbarra
    • Teorema di Huygens-Steiner
    • Energia cinetica per i corpi rigidi
    • Teorema di Koenig
    • Accelerazione di una sbarra


  • 29/11/2018 Coppia, potenza e momento d'inerzia

    • Coppia di forze e momento
    • Lavoro e potenza
    • Lavoro nel caso di rotazioni
    • Potenza nelle rotazioni
    • Calcolo del momento d'inerzia di un disco
    • Calcolo del momento d'inerzia di una sfera
    • Calcolo del momento d'inerzia di un disco bucato


  • 4/12/2018 Fluidostatica

    • Densità
    • Pressione
    • Legge di Stevino
    • Liquidi in rotazione
    • Barometro
    • Spinta di Archimede
    • Tubi di flusso
    • Equazione di continuità


  • 6/12/2018 Fluidodinamica e temperatura

    • Modello molecolare di un gas
    • Tubo di flusso
    • Ruote a pale, reversibilità, quasistaticità e massima efficienza
    • Fluidi ideali (Newtoniani), viscosità
    • Teorema di Bernoulli
    • Applicazioni (venturimetro, tubo di Pitot)
    • Temperatura. Sensazione. Termometro
    • Termometri a gas (ideali). Temperatura assoluta. Zero della temperatura. Scala kelvin
    • Legge dei gas perfetti
    • Calore. Definizione pratica (caloria). Capacità termica. 
    • Conduzione, convezione, irraggiamento (cenni)


  • 11/12/2016 Calore e temperatura

    • Coordinate termodinamiche
    • Dilatazione termica
    • Gradi di libertà
    • Capacità termica
    • Pareti diatermiche (conduttrici) e adiabatiche (isolanti)
    • Calore specifico
    • Irraggiamento. Leggi di Stefan e di Wien
    • Modello meccanico del gas perfetto
    • Temperatura ed energia cinetica per grado di libertà e per particella
    • Energia meccanica (ordinata) e calore (disordinata)
    • Conduzione. Legge di Fourier
    • Convezione. Legge di Newton
    • Diagramma di Clapeyron (PV)
    • Trasformazioni quasi statiche
    • Isoterma di un gas perfetto
    • Trasformazioni Isocore e isobare


  • 13/12/2018 Primo principio della termodinamica

    • Pressioni parziali di un gas. Legge di Dalton
    • Lavoro di un fluido. Integrale di pdV
    • Trasformazioni reversibili di un sistema adiabatico. Energia interna
    • Trasformazione di lavoro in calore. Esperimento di Joule. Equivalente meccanico della caloria
    • Primo principio della termodinamica. Conservazione dell'energia
    • Calore specifico a volume e pressione costanti. Caso dei gas perfetti. 
    • Trasformazioni adiabatiche
    • Ciclo di Carnot


  • 18/12/2018 Secondo principio della termodinamica

    • Enunciati di Clausius e Kelvin. Loro equivalenza
    • Rendimento di una macchina termica. Reversibilità e massima efficienza. Equivalenza delle macchine reversibili. 
    • Ciclo di Carnot. Calcolo del lavoro. Rendimento
    • Temperatura termodinamica. 
    • Teorema di Clausius. Entropia. 
    • Legge dell'aumento dell'entropia per sistemi chiusi.
    • Entropia, temperatura e calore nell'analogia con le ruote idrauliche. Vedere anche http://fisicax.complexworld.net/dove-si-nasconde-la-fisica/lindizio-del-mulino-e-del-fonone


  • 20/12/2018 Secondo principio, meccanica statistica e gravitazione

    • Simulazioni: dinamica molecolare e Monte Carlo
    • Integrali stocastici: calcolare pi greco
    • Medie temporali, distribuzioni di probabilità, medie stocastiche
    • La meccanica statistica: principio di minima informazione
    • Entropia di informazione (Shannon)
    • Livelli quantistici di una buca di potenziale
    • Calore e lavoro a livello microscopico
    • Leggi di Keplero e collegamento con le leggi di Newton